Copyright © 2007-2018 Russ Dewey
Problem Solving
Virtually all cognitive activity resembles problem solving, the task of moving a system from its current state A to a goal state B. Any successful cognitive act (retrieving a memory, perceiving a scene, understanding a passage) can be seen as a goal-directed behavior.
In visual perception, the goal is to come up with a construction that accurately describes the sensory world. For example, in our description of visual scene analysis, the goal was to find a way to interpret visual clues like surfaces and edges in which all the data fits together into one coherent interpretation. That ws the constraint-satisfaction approach.
In language comprehension, the problem is to reconstruct the author's intended meaning. Again, the product of cognition is guided by multiple sources of information. Ambiguous words must be resolved in a process very much like analyzing a visual scene: all the clues must fit together.
In motor activity, the problem is to arrive at a destination or manipulate an object in a particular way. To solve the problem, one must find a sequence of intermediary actions that results in the goal state.
In what sense does all cognition require problem solving?
Here are two examples of problem solving from very different realms. They are similar processes in that each presents the brain with the dilemma of how to move from state A to state B.
1. Problem: get a college degree. The problem is to move yourself from state A (where you are now) to state B (completing your degree requirements) so you can graduate from State U or wherever you are going to school. This is done in a series of steps: completing basic courses, selecting a major, selecting appropriate higher-level courses in the major, and so on, removing each impediment to graduation, one by one.
2. Problem: interpret your view of the room after closing your eyes and rolling your head back then opening your eyes again. The problem is to come up with a coherent interpretation of your visual world after performing a disorienting maneuver. Your brain has to go from state A (opening your eyes and experiencing an unusual visual pattern) to state B (figuring out what you are looking at, getting oriented, perceiving the room).
If you can see how both of these as examples are problem solving, then you understand what it means to say that, in a sense, all cognition is problem solving. It is all goal-directed activity.
Puzzles
Puzzles are problems that are difficult to solve because they require some unusual insight or unexpected mental operation. By definition, this means they do not succumb to the first mode of attack. They have proven difficult for at least some people.
Puzzles played a role in the history of cognitive psychology because they were simple to bring into a lab, standardized, and people differed dramatically in their speed of solving them. They were commonly used in mid-20th Century studies of problem-solving.
Example: Duncker's Candle Problem
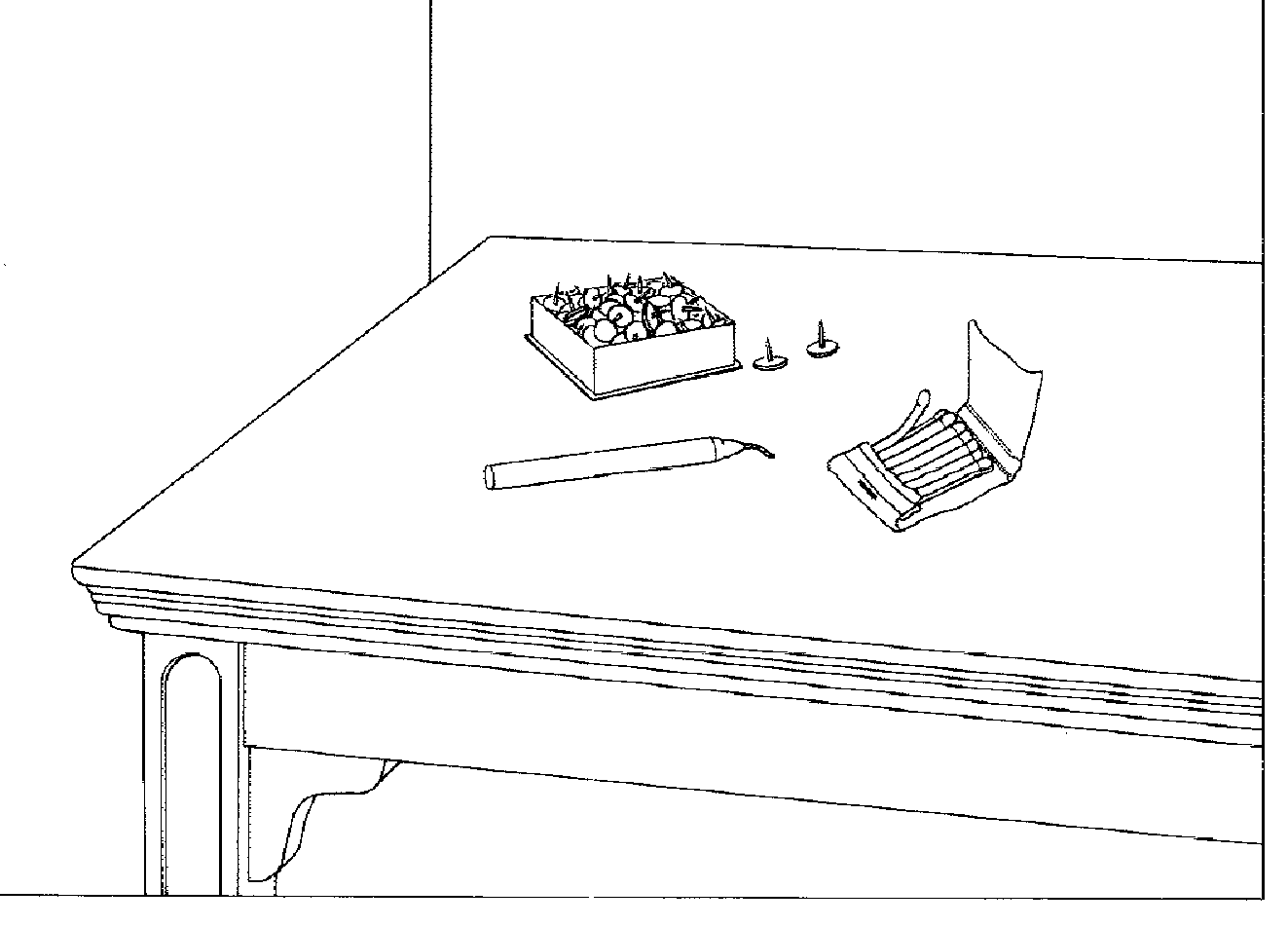
Duncker's (1945) candle problem
Suppose you were presented with a tabletop containing a box full of tacks, a candle, and a matchbook. Your challenge is to find some way to use these materials to mount a candle on the wall and illuminate the room. How can you do it?
Most people start thinking of typical ways to use the objects, such as pinning the candle to the wall...but that won't work...or lighting the candle and dripping wax onto the wall...but that won't work...
The solution, ultimately, involves reconceptualizing the container of the tacks as something other than a container. Treat it as a potential platform for the candle.
That is the trick for solving this puzzle. One can empty the box, use a tack to fasten the box to the wall, then drip some wax onto the box and mount the candle on the box. (Several hours later the room will be in flames, but Duncker never discussed that.)
Duncker used the term functional fixity to describe the tendency of people to regard a certain object as having one, fixed function. A box is for containing things. To solve the puzzle, one must break out of functional fixity and use the box in an unusual way, as a platform.
What is Duncker's candle problem? What was Duncker's "functional fixity" concept?
In an example of how simple puzzles like this could inspire research, Higgins and Chaires (1980) showed that subjects could be unconsciously primed to find the correct solution to the candle problem.
First they were asked to participate in a study about long-term memory. They saw slides of common objects.
For one group, these objects were described using the word of (for example, "a carton of eggs"). For the other group, the same objects were described using the word and (for example, "a carton and eggs").
Then both these groups and several control groups were asked to solve the Duncker's candle problem. Only 20% of subjects in the "of" group could solve the candle problem within 10 minutes. A full 80% of subjects in the "and" group were able to solve the problem within 10 minutes.
How was Duncker's candle problem used in research?
Why did changing one word have such a profound effect? Evidently the "and" group was led to think of objects presented together as separate entities. The "of" group was led to think of objects presented together as interacting wholes.
Neither group was aware that they had been primed for the puzzle-solving part of the experiment, so this is an example of how an unconscious or automatic form of processing can influence which ideas enter attention. If it is true.
I say "if it is true" because, writing in 2017 after the priming brouhaha, I am primed to wonder about possible failures in replicating priming studies. The effect is large (80% to 20%) to the point of being almost incredible for such a subtle verbal cue.
So there is a project for an ambitious psychology major: replicate the Higgens and Chaires (1980) study. See if you can arrange a double-blind version in which experimenters do not know who is in the "and" or "of" group, to eliminate any effects of expectancy.
In general, solving a puzzle requires (1) ignoring obvious solutions that do not work, and (2) trying out unusual approaches. To solve the problem one must locate a low-probability solution.
Not all puzzles are equally revealing of intelligence. Sternberg and Davidson (1982) point out that puzzles commonly require that you find a "trick," and that is not necessarily a sign of deep intelligence.
Puzzles that correlate with high IQ scores (they suggested) are those that present both relevant and irrelevant clues, requiring the puzzle solver to ignore obvious but irrelevant clues while trying out unusual solutions.
Thinking Outside the Box with the 9-Dot Problem
Here is another classic puzzle, the 9-dot problem. To a person who encounters it for the first time, it can be puzzling indeed.
The problem is to connect 9 dots (three evenly spaced rows of three) with four lines, without lifting your pencil from the paper. If you do not know the solution to this puzzle, you should try to solve it now, using trial and error, before you read further.

The Nine Dot problem: connect the dots by making four lines, without lifting your pencil from the paper
Again, to solve the puzzle, step outside the normal or expected pattern of responses. One must try unusual or low-probability alternatives.
All of this is logical if you think about what defines a puzzle. A puzzle is a problem for which the obvious response does not work.
Otherwise the situation would not be puzzling. So a puzzle always requires a person to think "outside the box."
Why is it logical that puzzle solving often requires a low-probability response?
In this case, the solution is to violate the common assumption that one must stay within the square defined by the dots. When you start experimenting with lines that extend outside the square, the answer usually comes quickly.
Here is one solution. If the dots are numbered 1 through 9, then draw a line from dot 1 through 5 to 9, then up through 6 and 3 and beyond, then back down through 2 and 4, then through 7 and 8.
The General Problem Solver
Before the modern era of cognitive research, problem solving was studied mainly through examination of humans with puzzles. The modern era of computer-based research on problem solving started with Newell and Simon (1963). They designed a computer program called the General Problem Solver (GPS).
Newell and Simon defined each problem as a space. At one end of the space is the starting point. On the other side is the goal.
In the General Problem Solver, the program tests various actions (called operators by Newell and Simon) to see which would take it closer to the goal state. An operator is any activity that changes the state of the system.
The General Problem Solver always chose the operator that would bring it closer to its goal. This tactic is called hill climbing, because it resembles the tactic of always heading uphill, if your goal is to climb a mountain.
How did the GPS (General Problem Solver) solve problems?
Similarly, humans struggle toward long-term objectives one step at a time. As you complete each phase of the project, you take one step closer to the goal. (You may recognize here the pattern of deviation-reducing feedback, discussed earlier in the context of motor activity.)
Hill climbing is a simple strategy, but it does not always work efficiently. One potential trap is the foothill problem.
What is hill-climbing? What is the foothill problem?
Suppose your goal is to climb a mountain. You could start far away from the mountain and simply select whatever step takes you uphill. But you might end up climbing a foothill that lies between yourself and the mountain.
That would be foolish because it would ignore a much more efficient procedure: go around the foothill. In other words, if you go straight toward a goal without flexibility, you may pay a steep price, waste a lot of energy, or cause more work for yourself without contributing to the long-term goal.
More sophisticated problem-solving programs look ahead many steps to locate potential problems in advance. Then they can evade hidden traps and inefficient foothills, to more efficiently climb the mountain.
Advice for Human Problem Solvers
Cognitive psychologist Wayne Wickelgren wrote a little book called How to Solve Problems (1974). It was based on a popular course on problem solving which he developed at MIT (the Massachusetts Institute of Technology).
The aim of the course was to present students with useful problem-solving principles. Here is a summary of the principles he developed. Of course, this summary is very compressed. Professor Wickelgren spent a whole semester conveying these points.
- Use inference. The information required to solve a problem is probably hidden, not obvious, otherwise it would not be a problem. Be ready to go beyond the information given, looking for solutions or partial solutions.
- Classify action sequences. . This means that you examine the actions required to accomplish a goal, put the actions into different categories, and generate more possibilities in each of those categories. Try different variations as needed to accomplish the goal.
For example, on the way to getting a top grade on a test, you must set up a schedule, find an environment to study, do the studying, and get into the best state of mind before a test. This analysis yields four sets of action sequences.
You could generate new ways to tackle each component, such as:
- variations in time management (altering your schedule, setting aside times to study, etc.)
- variations in environment (you might try the library, or a quiet room)
- variations in study tactics (write out answers, or read more slowly, or read more than once)
- variations in test-day tactics (relaxing yourself before a test, getting a good sleep the night before, preparing yourself with helpful self-coaching statements).
What does it mean to classify action sequences?
- Do "hill climbing." Hill climbing occurs when you keep a goal in mind and approach it step by step. It is a long-term strategy for accomplishing a larger goal by performing smaller actions that move you in the right direction.
For example, a successful diet or exercise program requires many small decisions and actions. The cumulative effect is large, if all lead in the same direction. - Make subgoals. Often problems are best solved by breaking them into pieces. Then you can try to solve each piece of the problem by itself.
A student might have to take a few lower-level courses to strengthen basic skills, before tackling a tough course in the major. - Try contradiction. "Cultivate the habit of seeing the alternative." When stuck on a problem, sometimes it helps to consider an opposite viewpoint.
- Try working backward. Sometimes a problem is easier to solve if you start with the goal, then work backwards from it.
Isaac Asimov, a prolific science fiction writer, said he commonly started with a conclusion in mind, then wrote a story leading to it. - Seek relations between different problems. A solution to a problem might be discovered by examining similar problems from the past.
Consulting an expert often helps. The expert is likely to be acquainted with a wide range of similar situations and can point to a relevant example or case history.
Constraint Satisfaction as a Problem-Solving Approach
Sometimes a problem requires picking the best option from available choices. A good general-purpose problem solving technique is this: list the constraints of a situation (negative constraints, like limitations, and positive or desirable elements wanted in the final solution). Then pick the choice that satisfies most of the constraints.
For example, suppose your first house is newly constructed and has no landscaping around it. You might identify these factors as relevant to good solutions to the landscaping problems:
- The grass, trees, or bushes should be hardy in your climate. You do not want them dying after a few years.
- The plants should not be too expensive, if you are on a budget.
- The trees and bushes should not require too much care, if you are not spending all your time gardening or working in the yard.
- Trees should shade the house during the summer (especially if you live in a warm climate) or let sun through in the winter (especially if you are in a cold climate).
- Trees and bushes might should look attractive and/or proivide fruit or nuts.
- Some plants are much better than others for privacy hedges or providing cover for small animals like rabbits.
- There might be forms of wildlife in your area that you wish not to attract, so you avoid certain plants.
- If you are putting plants along your foundation, you don't want plants that will outgrow their space in a few years; perhaps they should be dwarf species or comfortable with being cut back (etc).
How can constraint satisfaction be employed as a general problem solving technique?
As you evaluate landscaping alternatives, run through your checklist. See which of the available alternatives will meet the largest number of constraints.
A solution that satisfies multiple constraints at the same time is likely to be esthetically pleasing. It will be an elegant solution, and that will be satisfying.
---------------------
References:
Duncker, K. (1945). On problem solving. Psychological Monographs, 58, 1-113.
Higgins, E. T., & Chaires, W. M. (1980). Accessibility of interrelational constructs: Implications for stimulus encoding and creativity. Journal of Experimental Social Psychology, 16, 348-361.
Newell, A., Shaw, J. C., & Simon, H. A. (1959). Report on a general problem-solving program. Proceedings of the International Conference on Information Processing. Pp.256-264.
Sternberg, R. J. & Davidson, J. E. (1982, June). The mind of the puzzler. Psychology Today, 37~4.
Write to Dr. Dewey at psywww@gmail.com.
Don't see what you need? Psych Web has over 1,000 pages, so it may be elsewhere on the site. Do a site-specific Google search using the box below.
