Copyright © 2007-2018 Russ Dewey
Gestalt Psychology
A gestalt (pronounced ge-STALT with a hard "g" as in "get") is a pattern, thing, form, shape, or object: something whole. The word percept means about the same thing: an object of perception.
In the mid 20th Century, most American experimental psychologists were behaviorists. They believed psychological phenomena could be explained by referring only to observable behavior. There was no need to talk about things inside the head.
The Gestalt psychologists bristled at this idea. To them it seemed obvious that hidden processes within the brain were crucial to explaining perception.
To prove their point, Gestalt psychologists liked to show ambiguous figures. A famous example is the Peter/Paul Vase or Rubin Goblet, publicized by Danish psychologist Edgar Rubin in 1915.

The Rubin goblet
The picture can be seen as a vase-like object or as two faces. Two different perceptions could result from the same stimulus. To the gestalt psychologists, this clearly showed something was going on inside the head to determine which figure was seen at a given moment.
Therefore (they argued) perception involved more than just the stimuli that entered the eye. Measuring observable stimuli and responses was not enough. Central processes (brain processes) were involved.
What does the word gestalt mean? Why did ambiguous figures fascinate the Gestalt psychologists?
The gestalt psychologists of the 1930s and 1940s did not have the tools to develop this valid insight. They referred vaguely to fields in the brain that were isomorphic (equivalent in form) to the gestalts.
Today we are aware that computing machinery does not physically resemble the things being computed. We would not expect to find electrical fields resembling faces in a graphics chip processing information about faces.
However, the gestalt psychologists were correct that brain processes were involved in perception. The same stimulus could lead to two different perceptions, depending on those processes.
The Rubin Goblet illustrated a basic concept from Gestalt psychology: the figure-ground distinction. When a gestalt is formed (perceived) it becomes a figure (a thing apart, an entity or object).
A figure is always backed up by a surrounding ground. With Rubin's goblet, the goblet and faces take turns being figure and ground.
When you see the goblet, the faces disappear into a black background. When you see the faces, the goblet disappears into a white background.
A pattern cannot be seen as figure and ground at the same time. Yet the visual pattern of Rubin's Goblet does not change, only the brain's intepretation of it changes.
What is the difference between "figure" and "ground"?
To the gestalt psychologists, this proved that stimulus/response theories were inadequate to account for perception. That seemed like a vindication of their perspective.
Laws of Pragnanz
Kohler, one of the influential Gestalt psychologists, described laws of pragnanz that, he said, determined which gestalts would form from ambiguous stimuli. In German, pragnanz means clarity, so laws of pragnanz are laws of clarity.
A common translation of "laws of pragnanz" is laws of good form. A law of pragnanz identifies an organizational tendency, a way in which the human brain decides which things go together or belong in the same gestalt.
What is a "law of pragnanz"?
One of Kohler's laws of pragnanz involved similarity. Similarity among components encourages an observer to organize them into a figure. Proximity is another law of pragnanz mentioned by Kohler.
Proximity is closeness. Objects close to each other tend to be perceived together in one form or gestalt.
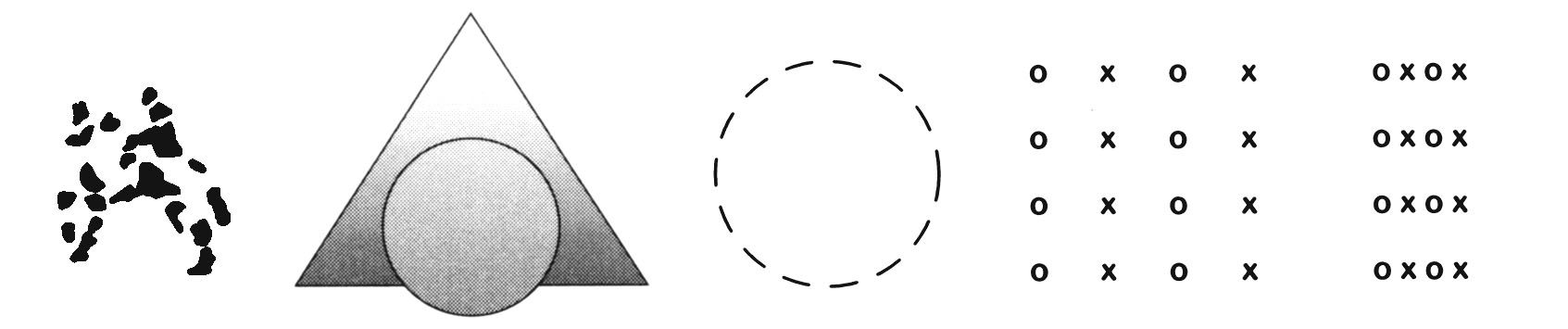
In order from left to right: closure, symmetry, continuity, similarity, and proximity.
In the first illustration, one can see a rider on a horse despite the fact that major portions of the figure are missing. This is called closure because the perceptual system closes the gaps needed to perceive a familiar form automatically.
The second example–the triangle behind the ball–illustrates the effect of symmetry and also continuity. Symmetry is present because the left and right halves of the triangle are mirror images of each other, so we naturally assume they are part of the same object. Continuity is illustrated because we assume the bottom edge of the triangle continues behind the ball.
The third example, the broken circle, illustrates continuity. The elements are seen as a circle rather than just line segments, because the segments are lined up in a continuous curve. The same figure illustrates closure because the continuity encourages us to fill in the gaps and see a circle.
The fourth example shows similarity, because we group similar items together. If you can make out the X's and O's (not easy on a very small display) you will tend to see four columns rather than four rows.
The fifth and last example shows the law of proximity or closeness. It is easier to see four rows rather than four columns, when the elements making up the rows are closer together.
What are the principles or laws of similarity, proximity, continuity, and closure?

A famous demonstration of closure
The dog with his nose to the ground is a famous example of closure. When you see the dog, it suddenly becomes solid. A gestalt is formed. Your perceptual system succeeds in connecting the dots, so to speak, and you perceive an object.
Our perceptual systems need this ability because often our view is partially blocked or obscured. Without closure, we could not recognize objects seen through a bush or a rainy window, or when other objects block part of our view.
Why is "closure" useful?
Because of the visual system's ability to create closure, humans are very good at creating a gestalt or perceptual object out of the mere suggestion of an object. Cartoonists exploit this talent with their very sketchy representations of people and objects, who we nevertheless recognize.
"The Whole is Other than the Sum of the Parts"

Kurt Koffka
When the perceptual system forms a percept or gestalt, the whole thing has a reality of its own, independent of the parts. The Gestalt psychologist Kurt Koffka made a famous statement about this: "The whole is other than the sum of its parts."
This statement is often translated to English as, "The whole is greater than the sum of the parts." Koffka did not like that translation. He firmly corrected students who substituted "greater" for "other" (Heider, 1977).
"This is not a principle of addition," he said. The statement was supposed to mean that the whole had an independent existence in the perceptual system.
What was Koffka's famous statement? Why did he often correct students?
Here is another example of how the whole is other than the sum of the parts. Consider the white triangle shown next. It is called a subjective contour because no triangle is objectively present, but you can see the edges of a white triangle.

A subjective contour
The triangle is a gestalt. It is a form that acts like an independent whole. It affects your interpretation of each individual component of the picture.
Look at the circles in the corners. If you cover everything except one circle, it does not look like a white corner over a black circle. It looks like the old video game character, Pac-Man.
When you view the triangle as a whole, the Pac-Man shape into a white corner over a black dot. The whole (the gestalt, the triangle-ness) influences your interpretation of the part.
By exerting this influence, the triangle shape acts like a separate thing. That is what Koffka was talking about when he said the whole was other than the sum of the parts.
How is Koffka's saying illustrated by the triangle?
Heygt, Peterhans, and Baumgartner (1984) showed that illusory contours led to the same distinctive brain response as real shapes. The perception of a triangle, the formation of a triangle gestalt, caused the same brain response as a triangular object in the outside world.
What did researchers discover about the brain's response to subjective contours?
---------------------
References:
Heider, G.M. (1977). More about Hull and Koffka. American Psychologist, 32, 383.
Heygt, R. V. D., Peterhans, E., & Baumgartner, G. (1984). Illusory contours and cortical neuron responses. Science, 224, 1260-1262.
Write to Dr. Dewey at psywww@gmail.com.
Don't see what you need? Psych Web has over 1,000 pages, so it may be elsewhere on the site. Do a site-specific Google search using the box below.
